Anatomia di una Relazione Algebrica e di un Metodo di Indagine Criptico
Scritto da Giovanni Princigalli, pubblicato
Pensando a un laboratorio di matematica dal titolo: Alla riscoperta della relazione di Erone con strumenti matematici insoliti. Il corpus di idee presenti nella relazione in oggetto è molto ampio. Com’è noto, essa permette di calcolare l’area di un triangolo qualsiasi, (A), con lati assegnati (\alpha, \beta, \gamma) e visto che:
può essere scritta:
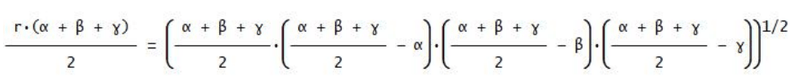
È composta con ingredienti alla portata di tutti coloro che abbiano un minimo di confidenza con la matematica. Gli elementi essenziali sono le variabili che rappresentano i lati di un generico triangolo piano e il raggio della circonferenza inscritta, uniti dalle quattro operazioni aritmetiche: somma, sottrazione, divisione, moltiplicazione, estrazione di radice e elevamento a potenza, oltre al segno di uguaglianza.
Sono tutte e sole le operazioni fondamentali del calcolo matematico che conferiscono alla relazione lo status di Teorema di Erone. Esso è inserito tra i dodici più famosi riportati nella pubblicazione di William Dunham.
Per le indagini successive è necessario operare una quadratura per eliminare la radice quadrata, operazione necessaria per quello che si dirà in seguito. Erone ha sviluppato per l’occasione un calcolo semplificato della radice quadrata e ha introdotto i numeri che portano il suo nome: numeri interi per i lati del triangolo affinché il radicando della formula risulti un quadrato perfetto (per esempio 12, 13, 5).
È evidente la relazione dei numeri di Erone con le terne pitagoriche. Eliminando la radice quadrata, però, bisogna evitare le terne di numeri che non rappresentano un triangolo.
Con piccoli accorgimenti algebrici si può ottenere l’espressione algebrica equivalente seguente, in forma implicita, che sarà indicata con E.
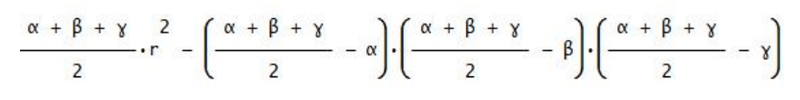
E è pronta per essere trattata con strumenti analitici differenziali. In parallelo con lo strumento standard sarà usato un secondo strumento che verrà presentato al momento opportuno per non appesantire la presente indagine preliminare.
Esso non ha ancora un nome, ma può essere ricavato facilmente per ogni data espressione algebrica usando il calcolo differenziale. Il calcolo differenziale è uno strumento eccellente per verificare se, in determinati contesti, e per qualche triangolo nel caso di E, si può ottenere l’annullamento della derivata prima o seconda.
La derivata, la prima, rispetto a una variabile fa pensare ai punti estremi, punti di massimo e minimo o di flesso. L’operazione di derivazione di E rispetto a una variabile è in effetti una derivata parziale - ma nel seguito continuerò a chiamarla derivata.
E non contiene espressamente operazioni differenziali, ma vista l’efficacia del calcolo nasce spontanea la sua applicazione a E per estrarre informazioni non visibili a prima vista. Ecco la derivata prima E’ di E, rispetto ad (\alpha), in forma implicita:
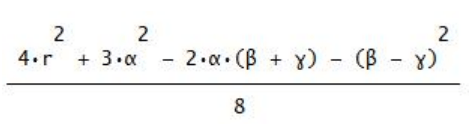
E’ è un oggetto interessante che non è facile associare all’immagine di pendenza tipica fornita dalla derivata di una funzione dipendente da una sola variabile. Con le precisazioni di cui sopra, calcolo anche la derivata seconda, E”.
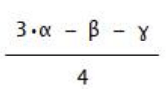
Per agevolare i calcoli algebrici con un computer, introduco il vettore [E, E', E''] che verrà confrontato con il vettore [E, I',I''] dove I’ e I” sono gli invarianti che entrano in gioco per la prima volta e che saranno meglio definiti in una prossima comunicazione. La presenza degli apici su I non significa che da I’ si passa a I” come si fa per passare da E’ a E”. È opportuno definire la funzione vettoriale:

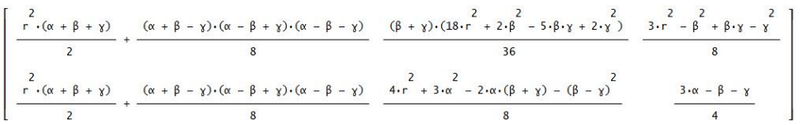
Per funzioni implicite a più variabili, la procedura per la ricerca degli estremanti deve seguire un diverso protocollo, ma in questo contesto divulgativo è importante soffermarsi su alcuni dettagli prima di definire correttamente gli invarianti I’ e I”.
Un generico triangolo con relativa circonferenza inscritta di raggio (r) può essere indicato così:
In presenza di angolo retto, usando le variabili (a, b), diventa:
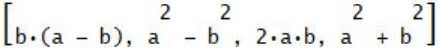
Il calcolo della relativa:
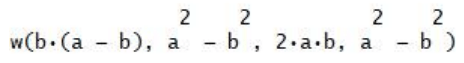
mostra, per (a=2b), i seguenti risultati:
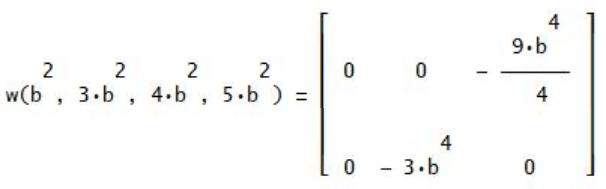
Si può notare che la prima colonna delle due righe della matrice di cui sopra mostra uno zero, ciò significa che per i triangoli considerati la formula di Erone è ovviamente verificata. Per (a=2b) si ottiene zero anche per I’, oltre che E”, quindi la quaterna
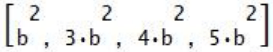
annulla E e I’. Per ora l’annullarsi di E” è da considerare solo una coincidenza.
Altri Casi Notevoli
La seguente classe di triangoli scaleni conferma il risultato precedente:
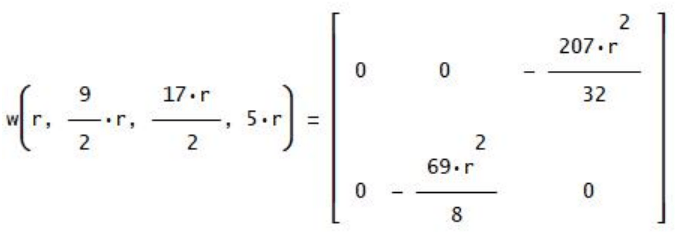
Invece, per la classe dei triangoli equilateri si ottiene:
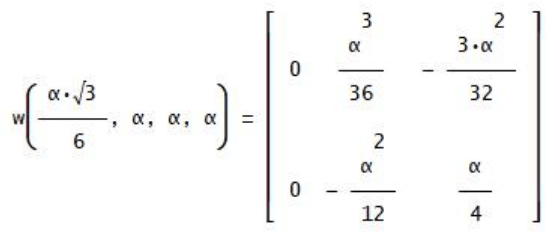
Si noti che, benché un triangolo equilatero sia ricco di simmetrie, la derivata prima, E’, è diversa da zero! Il seguente triangolo isoscele ripropone uno schema simile a quello relativo ai triangoli rettangoli già analizzato, eccolo:
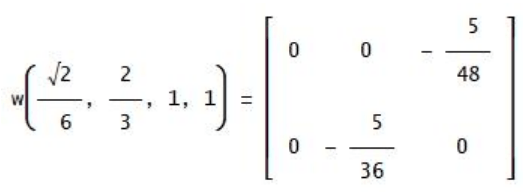
Una novità è rappresentata dal seguente triangolo isoscele:
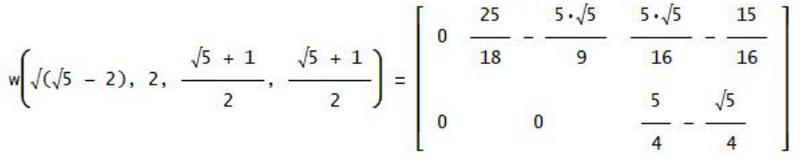
Un triangolo isoscele con misure speciali legate alla sezione aurea: visto il segno positivo della derivata seconda E”, dovrebbe essere considerato un punto di minimo?
Conclusioni Parziali in Attesa di Ulteriori Sviluppi
L’invariante I’ non pretende in alcun modo di sostituirsi alla relazione di E dalla quale discende. È comprensibile la situazione di rigetto che esso crea per il fatto che, come è stato mostrato in molti casi, si annulla come E quando utilizza tutte le altre variabili presenti in E, eccetto quella che in I’ non è presente per costruzione. In assenza di una dimostrazione generale, si può comunque dire che per l’ampia varietà di triangoli che soddisfano la formula di Erone e la relazione indicata come I’, non si può parlare di semplici coincidenze.
Di certo, I’ non può essere considerata indipendente dalla relazione dalla quale discende; forse deve essere vista come operazione su particolari simmetrie dei triangoli, una rottura di simmetria. La ricerca di senso in presenza del rigore deve essere abbinata a qualche altro criterio, forse all’immaginazione.
